
css之缓动函数
说缓动函数之前呢,先看下一个饿了么的css添加购物车的效果图,这是很多年前我使用纯CSS的bezier函数实现的, 本章主要探索贝塞尔曲线的使用和原理,下图项目的仓库在这里.

用CSS实现这样一个动画,在没有贝塞尔的帮助几乎是不可能实现的,而贝塞尔曲线很少有人关注可以配合CSS实现很多 炫酷的效果,实际上在一些细腻的, 符合真实物理反馈的交互动画上,可以配合选择出不同的物理效果,除了上面的购物车动画效果外,像下面这个滑动的按钮也可以用CSS实现。

# Bezier 曲线介绍
贝塞尔曲线最早在20世纪60年代,法国汽车工业时期发明的,主要也是为了解决车身的工业设计,因为汽车的图形是流线型的, 之后便一直沿用在计算机图形领域。
在计算机中可以计算两点间的直线距离,但曲线由于不确定性,是没有固定的算法表示的,这对在计算机中绘制矢量图形是非常重要的。 因为不管录入曲线信息和传输曲线信息,不可能靠点连成线的方法,而一定是靠着一种由推算规则完成的算法,可以减少很多的存储 和表达成本。这也是它出现的意义。

在贝塞尔二次曲线中,绘制一条曲线,通过不断计算t的位置,形成一条曲线,绿色的是调节点, 假如绿色的线不超过P0和P2,那么永远也不可能超过它们的象限。
所以单就Bezier曲线来说,它不是某一个特定技术的代名词,而是计算机中表示曲线的一种方法。不管做图表 ,动画,绘制不规则图形,都可以用这个方案来实现。
它也是绘制流线型曲线的最广泛方式,在 Adobe Illustrate 和 PS 中的曲线绘制都使用它来完成。
例如,在PS中的钢笔工具。
# 在CSS中的应用
在css中的动画中,有运动轨迹一说,从A点移动到B点时候,是保持线性平均速度,还是先快后慢,或者是先慢后快,可以通过 animation-timing-function, 或者transition-time-function属性来实现。它表示对某一个动画的运行轨迹。
如果要使用贝塞尔曲线的话,需要调用CSS的内置函数,cubic-bezier方法。
cubic-bezier 函数使用的是二次贝塞尔曲线,两个对点(p0和p3)带两个调节点(p1, p2),也就是四个参数,一般叫 P0 - P3。
需要注意的是,函数的参数是这么排列的, 不是从0-1,这么排列的好处是,一般P0和P3作为起始点和终点,不怎么调,P1和P2作为 调节点,会频繁改动,所以把P3放到了前边,便于查看和编写。
cubic-bezier(p0, p1, p3, p2)
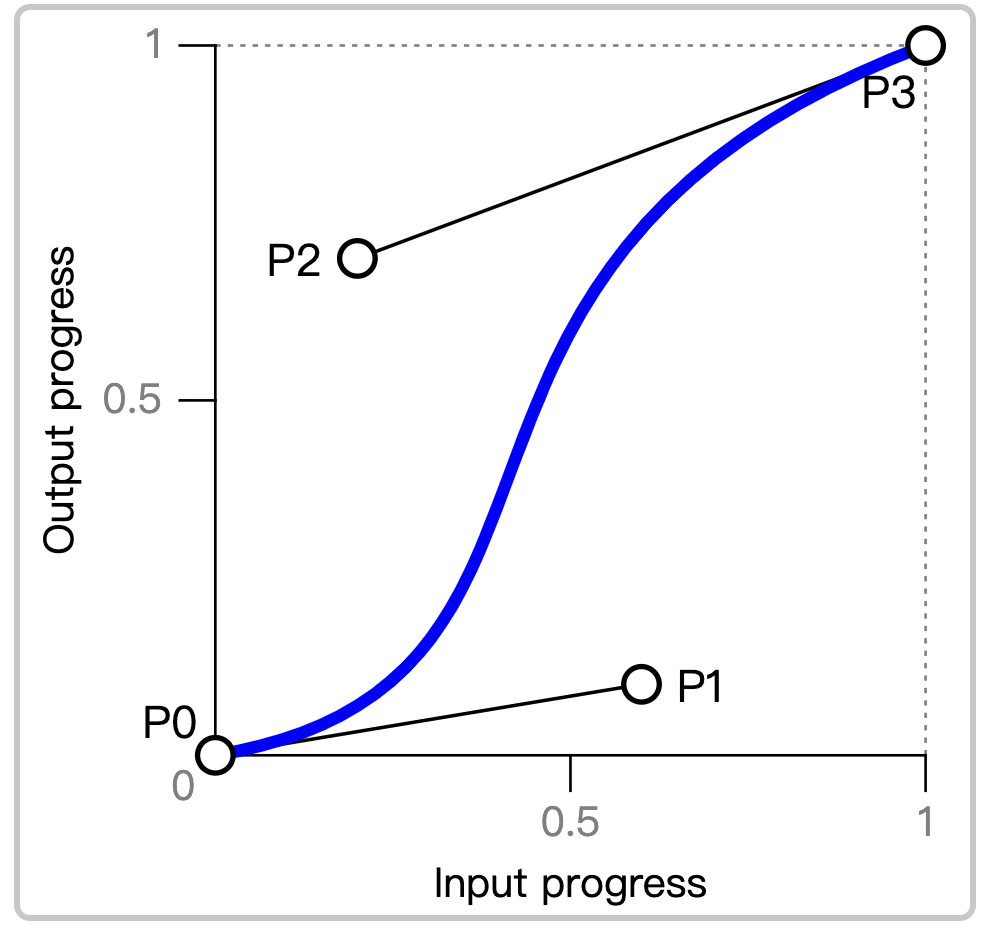
横轴表示时间,也就是P0,P3,从0-1。竖轴表示运动进度,一般是0-1,如果两个调节点都在1以内,不会使曲线超过设定的运动轨迹。也不会打乱原来的运行/时间的节奏。但如果超过了1之后,动画的运动就会变得溢出了。
什么叫溢出呢,假如一个球横向运动一个10S的动画,从0px移动到100px的位置,那么如果P1和P2设置成了4, 这个球的
动画部分依然运动到100px的位置,但是由于运行轨迹超出了1最大值,运动距离会相应的多出一部分(这部分不会算入动画部分内,只在运行时有对应峡谷),
整个运行时间不会发生改变。
也就是说,P1和P2可以超出1,但是超出后会对影响原来的动作执行时间,按照超出的程度,重新规划整个运动轨迹。
由于0,4,1,4是一个山峰型的轨迹,一个典型的快-慢-快的运行轨迹,我们就可以利用这个机制制作出CSS Animation 本身不能实现的不规则运动轨迹动画。 通过它,我们可以实现任何使用二次贝塞尔曲线可以画出的轨迹的动画。

会发现,由于0,1和1,1之间差了一个点,所以动画的没有平均分布在整个时间轴上,在尾部有点断层。这种情况可以使用big value hack的方式,最大化缩小0-1间的轴距。
比如我们用20来替代上面的4, 会变成下面的效果图。

有了曲线的运动方法,就可以利用多动画执行来实现多个方向的位移,下面这个就是利用x和y的两个动画实现山峰型的运行轨迹,x是正常动画,y是使用贝塞尔曲线。
# 总结: 应用场景和实用工具
饿了么加入购物车的动画效果和这个如出一辙,本质上都利用贝塞尔的不规则运动来突破 CSS Animation 实现不了的不规则运动限制。,可以通过贝塞尔曲线实现一些非平行的运行场景,一般分为ABC三个阶段,加入购物车的效果也是从快-慢-快只不过使用了贝塞尔曲线之后可以使DOM元素在位置上发生变化。
介绍一些常用的贝塞尔曲线生成工具,https://cubic-bezier.com/#0,0,1,1 是一个在线绘制贝塞尔曲线,即使浏览CSS效果的在线工具,常规的动画可以配合UI使用这个 工具研究一些自定义的运动效果。
如果是像上面的效果,在这个工具上不太好操作,需要手动调试,如果理解了二次贝塞尔的曲线规则,很容易脑补出运行轨迹,所以也不是什么难事。